Subject Infrastructure Repository
3| Get Access! |
| Home |
| SIR Software Objects |
| SIR Users and Publications |
| Frequently Asked Questions |
| Repository License |
| Acknowledgments |
Red Black Tree
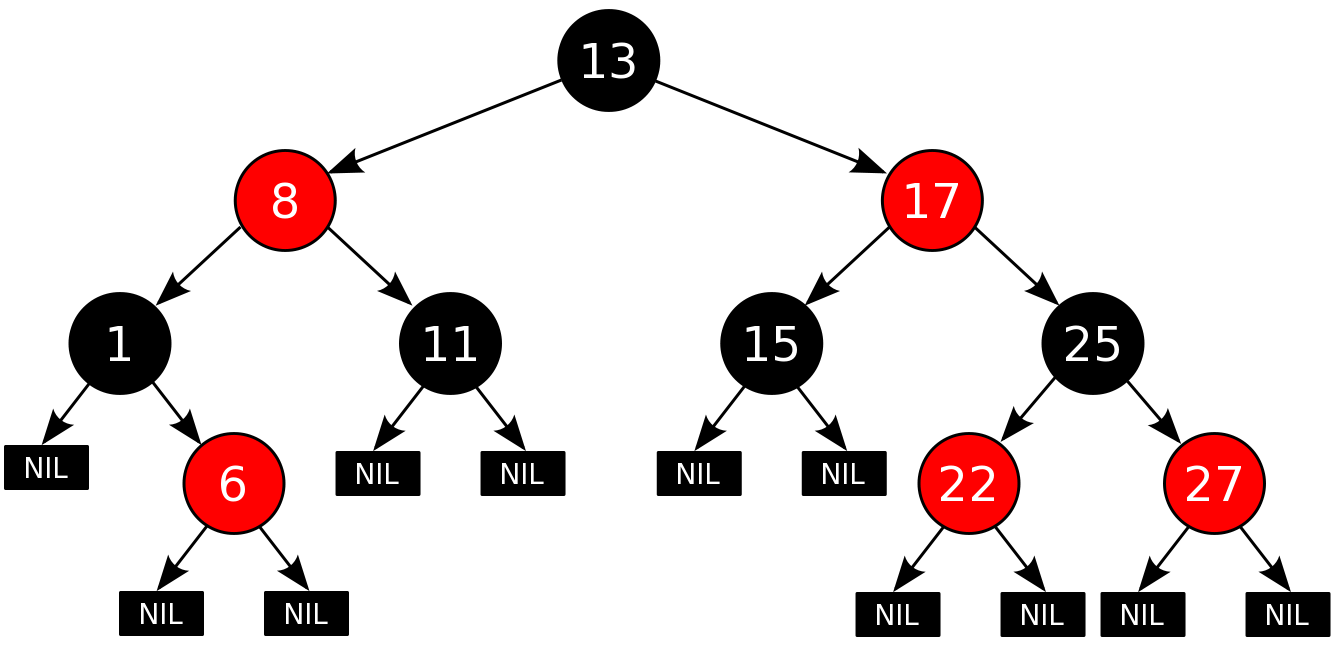
A red-black tree is a self balancing tree whose search/insert/remove methods have a time complexity of O(logn).
I. Language Agnostic Overview
Red-black trees are commonly used in programs when quick searching, inserting, or removing and efficient use of space are necessary. As they are the underlying data structure used in many more complex structures, scrutiny is warranted.
A red-black tree has all the constraints of a binary tree, and often can be used in the same way. However, a red-black tree also has several additional constraints:
Each node must be labeled either “red” or “black”.
The root node must be black.
All leaf nodes (null or sentinel values) must be black.
Both children of each red node must be black.
Every path from the root node to a leaf must contain the same number of black nodes.
A node's “black height” is defined as the number of internal black nodes in a path from the root to a leaf.
II. Java Specific Overview:
The red black tree is implemented with pointers (as opposed to on top of an array). There are five fields which are worth noting:
int key – This is the key accompanying the value that is to be searched for.
V value – This is the value itself, the data that the node is storing.
Entry<V> left – This is a pointer to the left child.
Entry<V> right – This is a pointer to the right child.
Entry<V> parent – This is a pointer to the node's parent.
wellConnected
a. This method verifies that the parent fields are correct.
b. This method has no preconditions or postconditions, rather it is used in verifying the conditions of other methods.
redConsistency
a. This method verifies that all the children of a red node are black.
b. This method has no preconditions or postconditions, rather it is used in verifying the conditions of other methods.
blackConsistency
a. This method verifies that all the children of a black node are red. It also verifies that the current node is black.
b. This method has no preconditions or postconditions, rather it is used in verifying the conditions of other methods.
ordered
a. This method verifies that all the order property still holds. That is, the keys of the left subtree of any node must be less than the node's key, and all of its right subtree as well.
b. This method has no preconditions or postconditions, rather it is used in verifying the conditions of other methods.
remove
a. This method finds and deletes the value with the given key. It then returns the value that was deleted. If the key could not be found, the data structure is not altered and null is returned.
b. The preconditions and postconditions, which are identical, both check that the root node is either null or the tree is consistently ordered, and that the data structure's size variable is correctly set to the size of the tree.
Metrics:
Lines of code for implementation: 334
Methods for implementation: 24
Lines of code for invariants: 96
Methods for invariants: 10
References:
Wikipedia's entry on red-black trees: http://en.wikipedia.org/wiki/Red_black_tree
Try the following link to upgrade the page display. (Explanation)